实验八

实验内容

1、一阶微分
x11.11.2
f(x)0.250.22650.2066
用三点公式计算f'(x)在x = 1，1.1，1.3的值。
2、用梯形公式计算积分并给出误差估计。
3、用三点辛普森公式计算积分并给出误差估计。
3、用程序说明三点辛普森公式其代数精度是3。
4、用梯形公式和指令 trapz 实现梯形公式求积法, 计算cos(x)在区间[0,π]的结果，并变换节点数, 用表列出积分的变化结果。


实验综述

本实验均基于 MATLAB 2019b 版本

安装MATLAB 2019b 点击查看

实验过程

一阶微分
x11.11.2
f(x)0.250.22650.2066
用三点公式计算f'(x)在x = 1，1.1，1.3的值

实验代码
%% 用三点公式计算f'(x)在x=1.0,1.1,1.3的值
%  版本 2019b

%% 代码部分
clc,close,clear;
x = [1.0,1.1,1.2];
y = [0.25,0.2268,0.2066];
n = length(x);
f1(1) = (-3*y(1)+4*y(2)-y(3))/(2*(x(2)-x(1)));  %三点公式求导数值
f1(2) = (y(3)-y(1))/(2*(x(2)-x(1)));
f1(n) = (y(n-2)-4*y(n-1)+3*y(n))/(2*(x(2)-x(1)));
fprintf('f(x)在x=1,1.1,1.2的导数值分别为：\n');
disp(f1);
% 根据二次插值多项式求导得出f(x)在x=1.3的导数值
P = @(a) y(1)*(2*a-x(2)-x(3))/(2*(x(2)-x(1))^(2))-y(2)*(2*a-x(1)-x(3))/((x(2)-x(1))^(2))+y(3)*(2*a-x(1)-x(2))/(2*(x(2)-x(1))^(2));
fprintf('f(x)在x=1.3的导数值为：\n');
disp(P(1.3));
实验效果

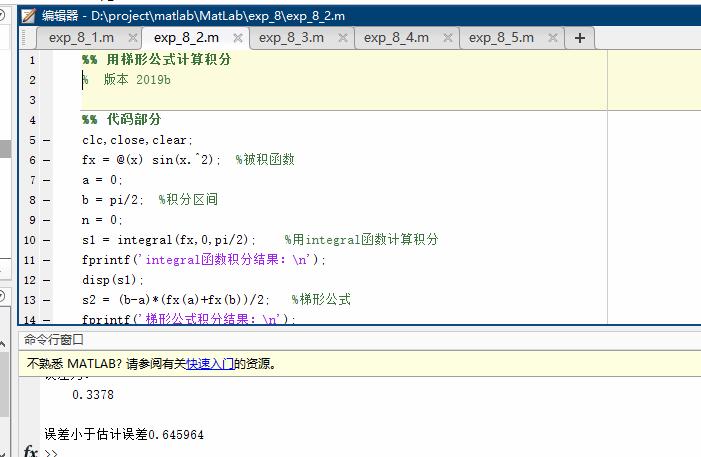
用梯形公式计算积分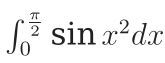并给出误差估计

实验代码
%% 用梯形公式计算积分
%  版本 2019b

%% 代码部分
clc,close,clear;
fx = @(x) sin(x.^2);  %被积函数
a = 0;
b = pi/2;  %积分区间
n = 0;
s1 = integral(fx,0,pi/2);    %用integral函数计算积分
fprintf('integral函数积分结果：\n');
disp(s1);
s2 = (b-a)*(fx(a)+fx(b))/2;   %梯形公式
fprintf('梯形公式积分结果：\n');
disp(s2);
err = abs(s1-s2);   %计算误差
fprintf('误差为：\n');
disp(err);
syms x
d = diff(sin(x.^2),2);
M2 = subs(d,x,0);
ERR = eval(M2*((b-a)^(3))/12);  %估计误差计算公式
if abs(err) <= abs(ERR)
    fprintf('误差小于估计误差%f\n',ERR);
else
    fprintf('误差大于估计误差%f\n',ERR);
end
实验效果

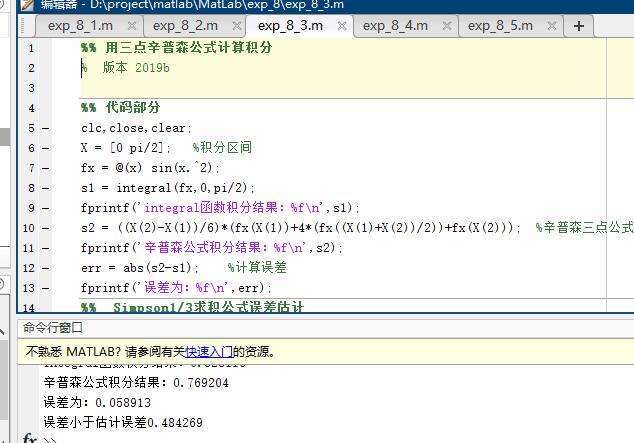
用三点辛普森公式计算积分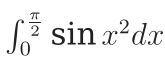并给出误差估计

实验代码
%% 用三点辛普森公式计算积分
%  版本 2019b

%% 代码部分
clc,close,clear;
X = [0 pi/2];   %积分区间
fx = @(x) sin(x.^2);
s1 = integral(fx,0,pi/2);
fprintf('integral函数积分结果：%f\n',s1);
s2 = ((X(2)-X(1))/6)*(fx(X(1))+4*(fx((X(1)+X(2))/2))+fx(X(2)));  %辛普森三点公式
fprintf('辛普森公式积分结果：%f\n',s2);
err = abs(s2-s1);    %计算误差
fprintf('误差为：%f\n',err);
%%  Simpson1/3求积公式误差估计
syms x
d = diff(sin(x.^2),4);
M = subs(d,x,pi/2);
ERR = eval(M*((X(2)-X(1))^(5))/2880);  %估计误差计算公式
if abs(err) <= abs(ERR)
    fprintf('误差小于估计误差%f\n',ERR);
else
    fprintf('误差大于估计误差%f\n',ERR);
end
实验效果

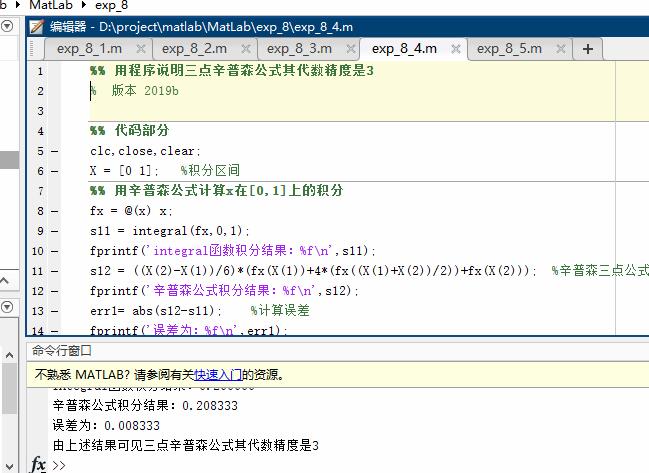
用程序说明三点辛普森公式其代数精度是3

实验代码
%% 用程序说明三点辛普森公式其代数精度是3
%  版本 2019b

%% 代码部分
clc,close,clear;
X = [0 1];   %积分区间
%% 用辛普森公式计算x在[0,1]上的积分
fx = @(x) x;
s11 = integral(fx,0,1);
fprintf('integral函数积分结果：%f\n',s11);
s12 = ((X(2)-X(1))/6)*(fx(X(1))+4*(fx((X(1)+X(2))/2))+fx(X(2)));  %辛普森三点公式
fprintf('辛普森公式积分结果：%f\n',s12);
err1= abs(s12-s11);    %计算误差
fprintf('误差为：%f\n',err1);
%% 用辛普森公式计算x^2在[0,1]上的积分
fx = @(x) x.^2;
s21 = integral(fx,0,1);
fprintf('integral函数积分结果：%f\n',s21);
s22 = ((X(2)-X(1))/6)*(fx(X(1))+4*(fx((X(1)+X(2))/2))+fx(X(2)));  %辛普森三点公式
fprintf('辛普森公式积分结果：%f\n',s22);
err2 = abs(s22-s21);    %计算误差
fprintf('误差为：%f\n',err2);
%% 用辛普森公式计算x^3在[0,1]上的积分
fx = @(x) x.^3;
s31 = integral(fx,0,1);
fprintf('integral函数积分结果：%f\n',s31);
s32 = ((X(2)-X(1))/6)*(fx(X(1))+4*(fx((X(1)+X(2))/2))+fx(X(2)));  %辛普森三点公式
fprintf('辛普森公式积分结果：%f\n',s32);
err3 = abs(s32-s31);    %计算误差
fprintf('误差为：%f\n',err3);
%% 用辛普森公式计算x^4在[0,1]上的积分
fx = @(x) x.^4;
s41 = integral(fx,0,1);
fprintf('integral函数积分结果：%f\n',s41);
s42 = ((X(2)-X(1))/6)*(fx(X(1))+4*(fx((X(1)+X(2))/2))+fx(X(2)));  %辛普森三点公式
fprintf('辛普森公式积分结果：%f\n',s42);
err4 = abs(s42-s41);    %计算误差
fprintf('误差为：%f\n',err4);
disp('由上述结果可见三点辛普森公式其代数精度是3');
实验效果

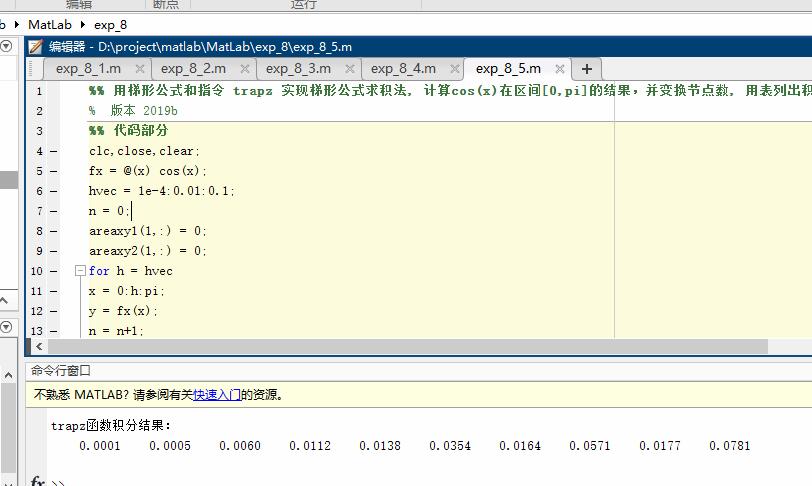
用梯形公式和指令 trapz 实现梯形公式求积法, 计算cos(x)在区间[0,π]的结果，并变换节点数, 用表列出积分的变化结果

实验代码
%% 用梯形公式和指令 trapz 实现梯形公式求积法, 计算cos(x)在区间[0,pi]的结果，并变换节点数, 用表列出积分的变化结果
%  版本 2019b
%% 代码部分
clc,close,clear;
fx = @(x) cos(x);
hvec = 1e-4:0.01:0.1;
n = 0;
areaxy1(1,:) = 0;
areaxy2(1,:) = 0;
for h = hvec
x = 0:h:pi;
y = fx(x);
n = n+1;
areaxy1(n) = h*(y(1)+y(end)+sum(2*y(2:end-1)))/2 ;  %梯形公式
areaxy2(n) = trapz(x,y);   % trapz函数
end
fprintf('x：\n');
disp(hvec);
fprintf('梯形公式积分结果：\n');
disp(areaxy1);
fprintf('trapz函数积分结果：\n');
disp(areaxy2);
实验效果