实验五
实验内容
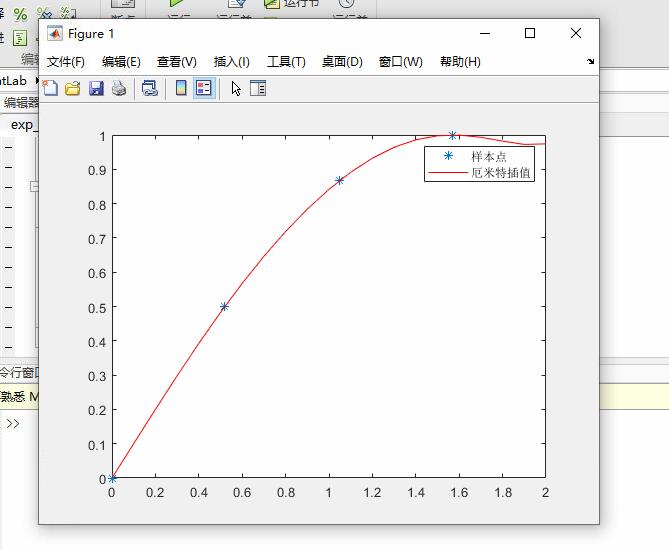
1、利用表中的数据给出分段厄米特插值结果:
| Xi | 0 | 0.52 | 1.047 | 1.57 |
| hXi | 0 | 0.50 | 0.866 | 1 |
| h'Xi | 1.00 | 0.866 | 0.500 | 0 |
3、使用 x = -3:3; y = [-1 -1 -1 0 1 1 1], 将 spline 和pchip 的插值结果进行比较并绘图。再采用振动采样函数,即执行 y=besselj(1,x), 重做前一步。
4、写出在 Matlab 中查询三次方样条数据插值 spline的步骤,并列出帮助中的所有语法? 采用数据 x = -4:4; y = [0 0.15 1.12 2.36 2.36 1.46 0.49 0.06 1] 做出样条函数并绘图。
5、多项式拟合: 已知 y = F(x) = 5 cos(x) + 0.5*randn(size(x)), x ∈[0, 3π], 从 y = F(x) 求出一组数据, 把 y = F(x) 拟合成三次多项式 P3(x) 的代码。
实验综述
本实验均基于 MATLAB 2019b 版本
安装MATLAB 2019b 点击查看
实验过程
利用表中的数据给出分段厄米特插值结果:
| Xi | 0 | 0.52 | 1.047 | 1.57 |
| hXi | 0 | 0.50 | 0.866 | 1 |
| h'Xi | 1.00 | 0.866 | 0.500 | 0 |
实验代码
%% 利用表43中的数据给出分段厄米特插值结果:
% Xi 0 0.52 1.047 1.57
% hXi 0 0.50 0.866 1
% h'Xi 1.00 0.866 0.500 0
% 版本 2019b
% 说明
%% 代码部分
clc,close,clear;
x = [0 0.52 1.047 1.57];
y = [0 0.50 0.866 1];
xq1 = [1.00 0.866 0.500 0];
X = 0:0.1:2;
p = hermite(x,y,xq1,X,1);
plot(x,y,'*',X,p,'r')
legend('样本点','厄米特插值')
%% 函数部分
%hermite.m
%求埃尔米特多项式和误差估计的MATLAB主程序
%输入的量:X是n+1个节点(x_i,y_i)(i = 1,2, ... , n+1)横坐标向量,Y是纵坐标向量,
%以f'(x_i)=y'_i(i = 1,2,...,n+1)为元素的向量Y1;
%x是以向量形式输入的m个插值点,M在[a,b]上满足|f~(2n+2)(x)|≤M
%注:f~(2n+2)(x)表示f(x)的2n+2阶导数
%输出的量:向量y是向量x处的插值,误差限R,2n+1阶埃尔米特插值多项式H_k及其系数向量
%H_c,误差公式wcgs及其系数向量Cw.
function[y,R,Hc,Hk,wcgs,Cw] = hermite(X,Y,Y1,x,M)
n = length(X);
m = length(x);
for t = 1 : m
z = x(t);
H = 0;
q = 1;
c1 = 1;
for k = 1 : n
s = 0;
V = 1;
for i = 1 : n
if k ~= i
s = s + (1/(X(k)-X(i)));
V = conv(V,poly(X(i)))/(X(k)-X(i));
end
end
h = poly(X(k));
g = ([0 1]-2 * h * s);%注意不要写成1-2*h*s,因为是多项式减法,低阶多项式前面必须用零填补
G = g * Y(k) + h * Y1(k);
H = H + conv(G,conv(V,V));%hermite插值多项式
b = poly(X(k));
b2 = conv(b,b);
q = conv(q,b2);
end
Hc = H;
Hk = poly2sym(H);
Q = poly2sym(q);
for i = 1 : 2*n
c1 = c1 * i;
end
wcgs = M * Q / c1;
Cw = M * q / c1;
y(t) = polyval(Hc,x(t));
R(t) = polyval(Cw,x(t));
end
end实验效果
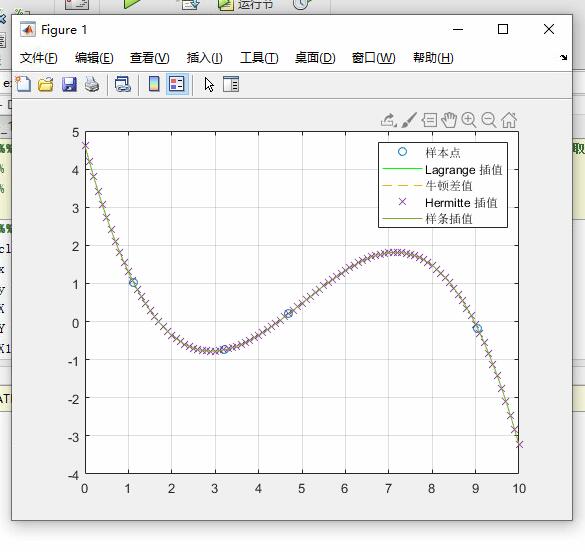
插值方法:从 y = F(x) = 5 cos(x) + 0.5randn(size(x)), x ∈[0, 3π] 中选取一些数据,在这些选取的数据上做 Lagrange 插值、牛顿差值、Hermitte 插值和样条插值
实验代码
%% 插值方法. 从 y = F(x) = 5 cos(x) + 0.5randn(size(x)), x ∈[0, 3π] 中选取一些数据,
% 在这些选取的数据上做 Lagrange 插值、牛顿差值、Hermitte 插值和样条插值。
% 版本 2019b
%% 代码部分
clc,close,clear;
x = 0:0.3:3*pi;
y = cos(x) + rand(size(x));
X = 3*rand(1,4)*pi;
Y = cos(X) + rand(size(X));
X1 = 0:0.1:10;
y1 = lagrange(X,Y,X1);
y2 = newton(X,Y,X1,1);
y3 = pchip(X,Y,X1);
y4 = spline(X,Y,X1);
plot(X,Y,'o',X1,y1,'g',X1,y2,'--',X1,y2,'x',X1,y2),grid
legend('样本点','Lagrange 插值','牛顿差值','Hermitte 插值','样条插值')
%% 函数部分
function yy=lagrange(x1,y1,xx)
%本程序为Lagrange1插值,其中x1,y1
%为插值节点和节点上的函数值,输出为插值点xx的函数值,
%xx可以是向量。
syms x
n=length(x1);
for i=1:n
t=x1;t(i)=[];L(i)=prod((x-t)./(x1(i)-t));% L向量用来存放插值基函数
end
u=sum(L.*y1);
p=simplify(u); % p是简化后的Lagrange插值函数(字符串)
yy=subs(p,x,xx); %p是以x为自变量的函数,并求xx处的函数值
end
function[y,R,A,C,L] = newton(X,Y,x,M)
n = length(X);
m = length(x);
for t = 1 : m
z = x(t);
A = zeros(n,n);
A(:,1) = Y';
s = 0.0; p = 1.0; q1 = 1.0; c1 = 1.0;
for j = 2 : n
for i = j : n
A(i,j) = (A(i,j-1) - A(i-1,j-1))/(X(i)-X(i-j+1));
end
q1 = abs(q1*(z-X(j-1)));
c1 = c1 * j;
end
C = A(n, n); q1 = abs(q1*(z-X(n)));
for k = (n-1):-1:1
C = conv(C, poly(X(k)));
d = length(C);
C(d) = C(d) + A(k,k);%在最后一维,也就是常数项加上新的差商
end
y(t) = polyval(C,z);
R(t) = M * q1 / c1;
end
L = poly2sym(C);
end实验效果
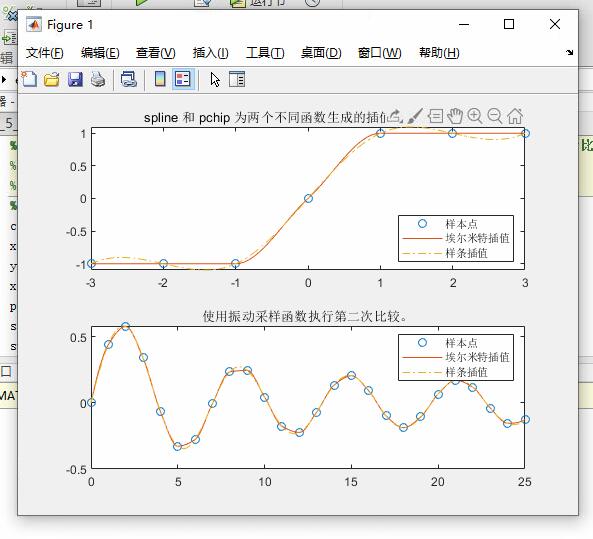
使用 x = -3:3; y = [-1 -1 -1 0 1 1 1], 将 spline 和pchip 的插值结果进行比较并绘图。再采用振动采样函数,即执行 y=besselj(1,x), 重做前一步
实验代码
%% 使用 x = -3:3; y = [-1 -1 -1 0 1 1 1], 将 spline 和pchip 的插值结果进行比较并绘图。
% 再采用振动采样函数,即执行 y=besselj(1,x), 重做前一步。
% 版本 2019b
%% 代码部分
clc,close,clear;
x = -3:3;
y = [-1 -1 -1 0 1 1 1];
xq1 = -3:.01:3;
p = pchip(x,y,xq1);
s = spline(x,y,xq1);
subplot(2,1,1);
plot(x,y,'o',xq1,p,'-',xq1,s,'-.')
title('spline 和 pchip 为两个不同函数生成的插值结果进行比较')
legend('样本点','埃尔米特插值','样条插值','Location','SouthEast')
x = 0:25;
y = besselj(1,x);
xq2 = 0:0.01:25;
p = pchip(x,y,xq2);
s = spline(x,y,xq2);
subplot(2,1,2)
plot(x,y,'o',xq2,p,'-',xq2,s,'-.')
title('使用振动采样函数执行第二次比较。')
legend('样本点','埃尔米特插值','样条插值')实验效果
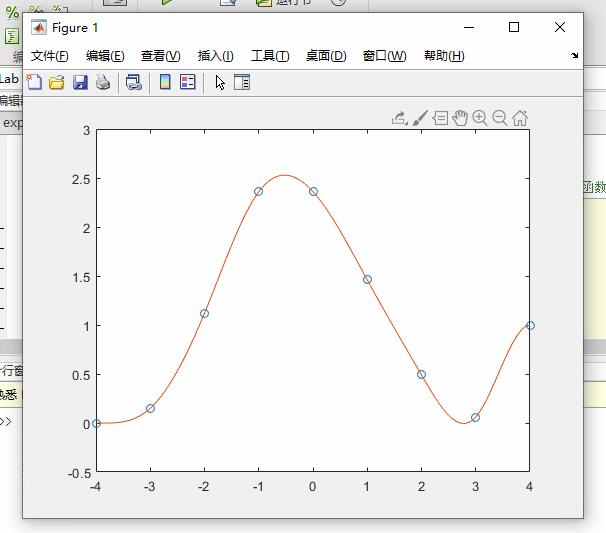
写出在 Matlab 中查询三次方样条数据插值 spline的步骤,并列出帮助中的所有语法? 采用数据 x = -4:4; y = [0 0.15 1.12 2.36 2.36 1.46 0.49 0.06 1] 做出样条函数并绘图
实验代码
%% 写出在 Matlab 中查询三次方样条数据插值 spline的步骤,并列出帮助中的所有语法?
% 采用数据 x = -4:4; y = [0 0.15 1.12 2.36 2.36 1.46 0.49 0.06 1] 做出样条函数并绘图。
% 版本 2019b
% 说明 :三次方样条数据插值 spline共有俩种
% s = spline(x,y,xq)
% pp = spline(x,y)
% s = spline(x,y,xq) 返回与 xq 中的查询点对应的插值 s 的向量。s 的值由 x 和 y 的三次样条插值确定。
% pp = spline(x,y) 返回一个分段多项式结构体以用于 ppval 和样条实用工具 unmkpp。
% 输入参数:
% x 坐标:指定为向量。向量 x 指定提供数据 y 的点。x 的元素必须是唯一的。 数据类型: single 或 double
% y 坐标:在 x 坐标处的函数值,指定为数值向量、矩阵或数组。x 和 y 通常具有相同的长度,但 y 也可以比 x 正好多出两个元素,用以指定端点斜率。
% 如果 y 是矩阵或数组,则在获取最后一个维度 y(:,...,:,j) 中的值时应使其匹配 x。
% 在此情况下,y 的最后一个维度的长度必须与 x 相同或正好多出两个元素。
% 三次样条的端点斜率遵循以下规则:
% 如果 x 和 y 是大小相等的向量,则使用非节终止条件。
% 如果 x 或 y 为标量,则会将该标量扩展为与另一方具有相同的长度并使用非节终止条件。
% 如果 y 是一个包含的值比 x 具有的条目多两个的向量,则 spline 使用 y 中的第一个和最后一个值作为三次样条的端点斜率。
% 例如,如果 y 是一个向量,则:
% y(2:end-1) 给出 x 中每个点处的函数值
% y(1) 给出区间开始处 min(x) 的斜率
% y(end) 给出区间结束处 max(x) 的斜率
% 同样,如果 y 是一个矩阵或 size(y,N) 等于 length(x)+2 的 N 维数组,则:
% y(:,...,:,j+1) 给出 x 中每个点的函数值,其中 j = 1:length(x)
% y(:,:,...:,1) 给出区间开始处 min(x) 的斜率
% y(:,:,...:,end) 给出区间结束处 max(x) 的斜率
% 数据类型: single | double
% xq - 查询点 向量 查询点,指定为一个向量。xq 中指定的点是 spline 计算出的插值函数值 s 的 x 坐标。 数据类型: single | double
%% 代码部分
clc,close,clear;
x = -4:4;
y = [0 0.15 1.12 2.36 2.36 1.46 0.49 0.06 1];
cs = spline(x,[0 y 0]);
xx = linspace(-4,4,101);
plot(x,y,'o',xx,ppval(cs,xx),'-');实验效果
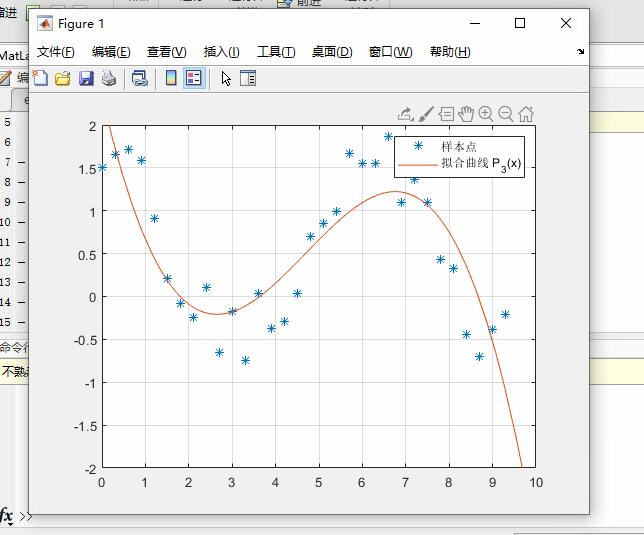
多项式拟合: 已知 y = F(x) = 5 cos(x) + 0.5*randn(size(x)), x ∈[0, 3π], 从 y = F(x) 求出一组数据, 把 y = F(x) 拟合成三次多项式 P3(x) 的代码
实验代码
%% 多项式拟合:
% 已知 y = F(x) = 5 cos(x) + 0.5*randn(size(x)), x ∈[0, 3π],
% 从 y = F(x) 求出一组数据, 把 y = F(x) 拟合成三次多项式 P3(x) 的代码。
% 版本 2019b
%% 代码部分
clc,close,clear;
x = 0:0.3:3*pi;
y = cos(x) + rand(size(x));
P3 = polyfit(x,y,3);
P3d = poly2str(P3,'x') %三次拟合多项式
plot(x,y,'*'),grid,hold
fplot(@(x) P3(1)*x^3 + P3(2)*x^2 + P3(3)*x + P3(4),[0 10])
axis([0 10 -2 2])
legend('样本点','拟合曲线 P_3(x)')实验效果